Random Forest Introduction

Random Forest Introduction

Random forest is one of popular algorithm which is used for classification and regression as an ensemble learning. It means random forest includes multiple decision trees which the average of the result of each decision tree would be the final outcome for random forest. There are some drawbacks in decision tree such as over fitting on training set which causes high variance, although it was solved in random forest by the aid of Bagging (Bootstrap Aggregating). Now firstly it is better to pay attention to decision tree algorithm and then study about random forest. Because random forest is divided to multitude decision tree.

Decision Tree:

Decision tree uses tree-like graph to take as best as possible decision by considering all elements of graph. For instance, remember tennis player who has agenda to play in different weather conditions. And now we want to know if player will play on 15th day or not?

Finding Pure Branch

There are 15 days which in 9 days he played and in 5 days he did not play; and now we want to know whether he plays in specific situation or not. You should look at train data carefully, there are different features with different values. We must see if for all of which value of which feature (Play = Yes for all days or Play = No) or in better word, which value is in the same color for above table.

(Humidity = High  For all days: (Play = Yes) | (Play = No)) No

(Humidity = Normal  For all days: (Play = Yes) | (Play = No)) No

(Wind = Weak  For all days: (Play = Yes) | (Play = No)) No

(Wind = Strong  For all days: (Play = Yes) | (Play = No)) No

(Outlook = Rain  For all days: (Play = Yes) | (Play = No)) No

(Outlook = Sunny  For all days: (Play = Yes) | (Play = No)) No

(Outlook = Overcast  For all days: (Play = Yes) | (Play = No)) Yes √

So our player played always when in “outlook =overcast” (D3, D7, D12, D13); we should start from “outlook” feature to make branch hand our root. So next time we should care about “Outlook = Sunny” and try to find that which days play situation were complete yes or no, because we want to know if “humidity” or “wind” is next one. In D1, D2, D8, D9, D11; just in (D1, D2, D8) (Humidity = High) is in the same color or same value which this time (Play = No) Sunny: D1, D2, D8, D9, D11

1. Sunny: D1, D2, D8 & (Humidity = High)  (Play = No)

2. Sunny: D9, D11 & (Humidity = Normal)  (Play = Yes)

So our next branch is “Humidity” because of finding “Pure” value. Now, look at when

“Outlook = Rain” Rain: D4, D5, D6, D10, D14 1. Rain: D4, D5, D10 & (Wind = Weak)  (Play = Yes)

2. Rain: D6, D14 & (Wind = Strong)  (Play = no)

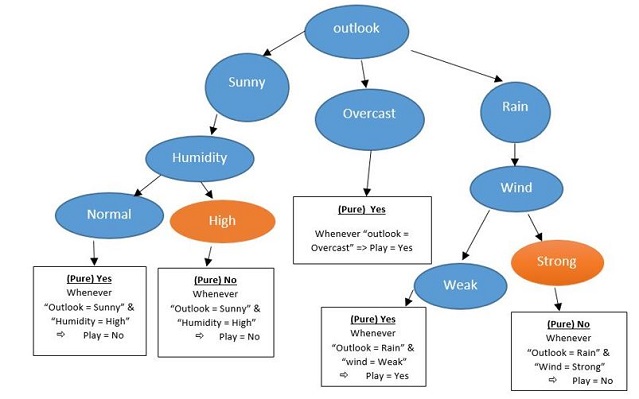
Now have a comparison of both table and decision tree in one glance:

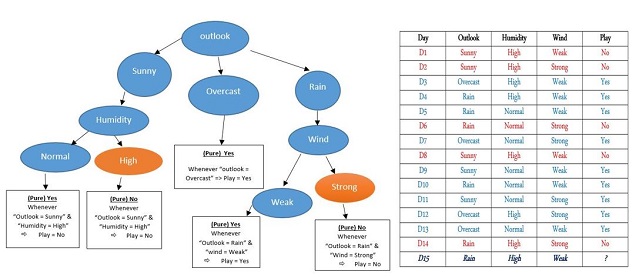
Therefore, for computing below situation, firstly we consider to “Outlook = Rain”, the new go through the right branch and check “Wind = Weak” so we go deep o let side which the answer is “Yes”. Hint: Over fitting definition; here in the below graph; as you saw, we have splitted each node until we achieve “Pure” result. For example, all of “Play” result should be same “Yes” or “No” in the last “leaf (end node of tree)”. If splitting continues until the end of pure set perfectly, then the accuracy will be 100%. It means each leaf in the end has just one specific value. The more splitting, we will have more accuracy and big tree, because tree grew up more and more. If tree size is as same as data set, then we have “over fitting”. Over fitting causes algorithm would be too specific to data (train) but it cannot generalize test data. How to avoid or stop over fitting is to prune tree, somehow remove branches which are not suitable and fit on future test data, then look at the result whether removing could hurt or improve our analyzing.

[ If (“outlook = Sunny” & “Humidity = Normal”  all of “Play = Yes”) ]

[ If (“outlook = Rain” & “wind = weak”  all of “Play = Yes”) ]

D15: “Outlook = Rain” & “Humidity=High” & “Wind=Weak”

Random Forest:

Random forest is an ensemble learning method which is very suitable for supervised learning such as classification and regression. In random forest we divided train set to smaller part and make each small part as independent tree which its result has no effect on other trees besides them. Random forest gets training set and divided it by “Bagging = Bootstrap Aggregating” which is algorithm to increase accuracy by prevent over fitting and decrease variance. It starts to divide data set to 60% as unique decision tree and 30% as overlapping data.

It divides train set to the “B” different decision tree (which 60% use unique data and 30% use duplicate data), then start to compute result or each decision tree and split them until appropriate situation (when it is enough for generalization for test data). In below you see that, there are two as “No” answers and three as “Yes” answers, so the average of answers is “Yes”.

Error Computation in Random Forest: There are some solutions to enhance random forest optimization. Cross Validation is to assess how the result of prediction model can generalize to another independent test data. There is train set as blew which has been divided to output as “Y” and features as “X”:

Bootstrapping:

Creating T trees randomly; T = { T1 , T2 , T3 , T4 , T5 } with replacement n times for each data. Out of Bag Error: If we consider randomly to specific j = (Xi , Yi) and looking for j in all of trees and find some trees which are without this value, so, they will be out of bag error. Indeed fraction of time when it repeats n times when (Xi , Yi) is not inside trees.